1.8 caTools一个奇特的工具集
问题
R除了统计,还能干什么?

引言
R语言生来就是自由的,不像Java,PHP等有统一的规范约束。R语言不仅命名、语法各包各异,就连功能也是各种混搭。caTools库就是这种混搭库,包括了不相关的几组函数工具集,有图片处理的,有编解码的,有分类器的,有向量计算的,有科学计算的,而且都很好用!以致于我都不知道,如何用简短的语言去描述这个包了!唯有“奇特”来概括它的特点。
1.8.1 caTools介绍
caTools是一个基础的工具包,包括移动窗口(Moving Window)统计,二进制图片读写,快速计算曲线的面积AUC,LogitBoost分类器,base64的编码器/解码器,快速计算舍入、误差、求和、累计求和等函数。
下面分别介绍caTools包中的API。
二进制图片读写
- read.gif & write.gif: gif格式图片的读写
- read.ENVI & write.ENVI: ENVI格式图片的读写,如GIS图片
base64的编码器/解码器:
- base64encode: 编码器
- base64decode: 解码器
注: Base64是一种基于64个可打印字符来表示二进制数据的表示方法。由于2的6次方等于64,所以每6个位元为一个单元,对应某个可打印字符。
快速计算曲线的面积AUC
- colAUC: 计算ROC曲线的面积(AUC)
- combs: 向量元素的无序组合
- trapz: 数值积分形梯形法则
LogitBoost分类器
- LogitBoost: logitBoost分类算法
- predict.LogitBoost: 预测logitBoost分类
- sample.split: 把数据切分成训练集和测试集
快速计算工具
- runmad: 计算向量中位数
- runmean: 计算向量均值
- runmin & runmax: 计算向量最小值和最大值
- runquantile: 计算向量位数
- runsd: 计算向量标准差
- sumexact, cumsumexact: 无误差求和,针对编程语言关于double类型的精度优化
1.8.2 caTools安装
本节使用的系统环境是:
- Linux: Ubuntu Server 12.04.2 LTS 64bit
- R: 3.0.1 x86_64-pc-linux-gnu
注:caTools同时支持Win7环境和Linux环境。
安装caTools包非常简单,只需要一条命令就可以完成。
~ R # 启动R程序
> install.packages("caTools") # 执行caTools安装命令
1.8.3 caTools使用
在R环境中,加载caTools类库
> library(caTools)
1. 二进制图片读写gif
a. 写一个gif图片
> write.gif(volcano, "volcano.gif", col=terrain.colors, flip=TRUE, scale="always", comment="Maunga Whau Volcano") #取datasets::volcano数据集,写入volcano.gif
b. 读一个gif图片到内存,再从内存输出
> y = read.gif("volcano.gif", verbose=TRUE, flip=TRUE) #读入图片到变量y
GIF image header
Global colormap with 256 colors
Comment Extension
Image [61 x 87]: 3585 bytes
GIF Terminator
> attributes(y) #查看变量的属性
$names
[1] "image" "col" "transparent" "comment"
> class(y$image) #查看图片存储矩阵
[1] "matrix"
> ncol(y$image) #列数
[1] 61
> nrow(y$image) #行数
[1] 87
> head(y$col,10) #颜色表,取前10个
[1] "#00A600FF" "#01A600FF" "#03A700FF" "#04A700FF" "#05A800FF" "#07A800FF" "#08A900FF"
[8] "#09A900FF" "#0BAA00FF" "#0CAA00FF"
> y$comment #查看图片备注
[1] "Maunga Whau Volcano"
> image(y$image, col=y$col, main=y$comment, asp=1) #通过y变量画图,如图1-19所示
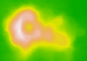 图1-19 火山地形图
图1-19 火山地形图
c. 创建一个git动画
> x <- y <- seq(-4*pi, 4*pi, len=200)
> r <- sqrt(outer(x^2, y^2, "+"))
> image = array(0, c(200, 200, 10))
> for(i in 1:10) image[,,i] = cos(r-(2*pi*i/10))/(r^.25)
> write.gif(image, "wave.gif", col="rainbow")
> y = read.gif("wave.gif")
> for(i in 1:10) image(y$image[,,i], col=y$col, breaks=(0:256)-0.5, asp=1)
在当前的操作目录,会生成一个 wave.gif 的文件,如图1-20所示。 动画演示效果参见本书在线资源中的文件wave.gif。
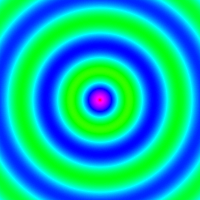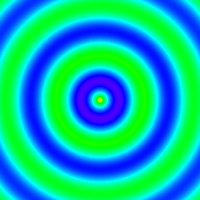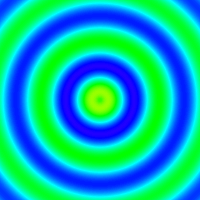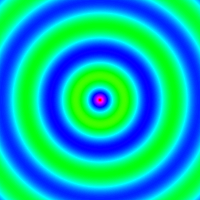
图1-20 同心圆变化动画
我们看到,caTools与谢益辉的animation包有一样的GIF输出动画功能。但使用caTools做gif动画,不需要依赖其他软件库。而animation的saveGIF函数需要依赖于ImageMagick或者GraphicsMagick等第三方软件。
2. Base64的编码器/解码器
Base64常用于处理文本数据的场合,表示、传输、存储一些二进制数据,包括MIME的email、email via MIME、在XML中存储复杂数据。Base64的编码解码,只支持向量(vector)类型,不支持data.frame和list类型。把一个boolean向量编解码,代码如下:
> size=1 #设置每个元素占用的字节数
> x = (10*runif(10)>5)
> y = base64encode(x, size=size)
> z = base64decode(y, typeof(x), size=size)
> x #原始数据
[1] FALSE FALSE FALSE FALSE TRUE TRUE FALSE FALSE FALSE FALSE
> y #编码后的密文
[1] "AAAAAAEBAAAAAA=="
> z #解码后的明文
[1] FALSE FALSE FALSE FALSE TRUE TRUE FALSE FALSE FALSE FALSE
把一个字符串编解码,代码如下:
> x = "Hello R!!" # character
> y = base64encode(x)
> z = base64decode(y, typeof(x))
> x #原始数据
[1] "Hello R!!"
> y #编码后的密文
[1] "SGVsbG8gUiEh"
> z #解码后的明文
[1] "Hello R!!"
错误测试:把一个数据框编解码
> data(iris)
> class(iris)
[1] "data.frame"
> head(x) #原始数据
| Sepal | Length Sepal | Width Petal | Length Petal | Width Species |
|---|---|---|---|---|
| 1 | 5.1 | 3.5 | 1.4 | 0.2 setosa |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 setosa |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 setosa |
| 5 | 5.0 | 3.6 | 1.4 | 0.2 setosa |
| 6 | 5.4 | 3.9 | 1.7 | 0.4 setosa |
> base64encode(x) #对数据框进行编码
Error in writeBin(x, raw(), size = size, endian = endian) :
can only write vector objects
3. ROC曲线
ROC曲线就是接收者操作特征曲线(receiver operating characteristic curve的简称,这是一种坐标图式的分析工具,主要用于选择最佳的信号侦测模型、舍弃次佳的模型和在同一模型中设定最佳阈值。ROC曲线首先由二战中的电子工程师和雷达工程师发明,用来侦测战场上的敌军载具(飞机、船舰等),即信号检测,之后很快就被引进心理学来进行信号的知觉检测。数十年来,ROC分析被用于医学、无线电、生物学、犯罪心理学等领域,而且最近在机器学习(machine learning)和数据挖掘(data mining)领域也得到了很好的发展。
取MASS::cats数据集,3列分别是Sex(性别)、Bwt(体重)、Hwt(心脏重量)。
> library(MASS)
> data(cats)
> head(cats)
Sex Bwt Hwt
1 F 2.0 7.0
2 F 2.0 7.4
3 F 2.0 9.5
4 F 2.1 7.2
5 F 2.1 7.3
6 F 2.1 7.6
> colAUC(cats[,2:3], cats[,1], plotROC=TRUE) #计算ROC的曲线面积AUC,输出图片,如图1-21所示
Bwt Hwt
F vs. M 0.8338451 0.759048
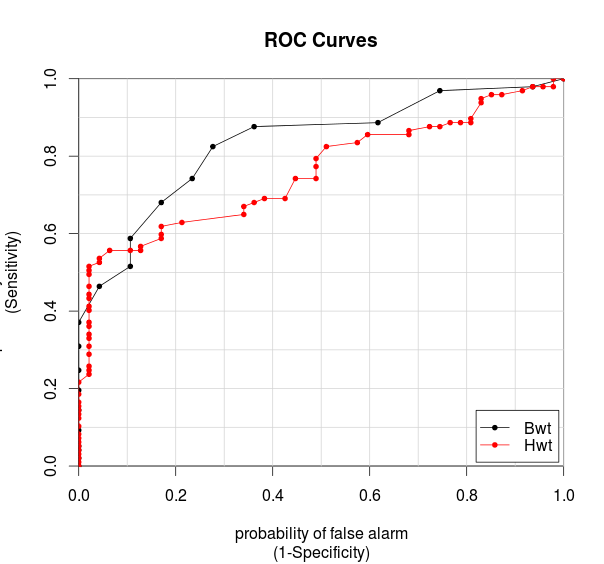
图1-21 ROC曲线
从AUC判断分类器(预测模型)优劣的标准:
- AUC = 1,是完美分类器,采用这个预测模型时,不管设定什么阈值都能得出完美预测。在绝大多数预测的场合,不存在完美分类器。
- 0.5 < AUC < 1,优于随机猜测。这个分类器(模型)如果妥善设定阈值的话,能有预测价值。
- AUC = 0.5,跟随机猜测一样(例如丢硬币),模型没有预测价值。
- AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
从图1-21我们看到Bwt和Hwt都在(0.5,1)之间,因此,cats的数据集是一个真实有效数据集。如果cats的数据集,是一个通过分类预测的数据集,用AUC对数据集的评分,就可以检验分类器的好坏了。
4. 向量元素的无序组合
combs(v,k)函数,用于创建无序的组合的矩阵,矩阵的列表示以几种元素进行组合,矩阵的行表示每种不同的组合。参数v是向量;k是数值,小于等于v的长度[1:length(v)]。
> combs(2:5, 3)
[,1] [,2] [,3]
[1,] 2 3 4
[2,] 2 3 5
[3,] 2 4 5
[4,] 3 4 5
> combs(c("cats", "dogs", "mice"), 2)
[,1] [,2]
[1,] "cats" "dogs"
[2,] "cats" "mice"
[3,] "dogs" "mice"
> a = combs(1:4, 2) #快速组合构建矩阵
> a
[,1] [,2]
[1,] 1 2
[2,] 1 3
[3,] 1 4
[4,] 2 3
[5,] 2 4
[6,] 3 4
> b = matrix( c(1,1,1,2,2,3,2,3,4,3,4,4), 6, 2)
> b
[,1] [,2]
[1,] 1 2
[2,] 1 3
[3,] 1 4
[4,] 2 3
[5,] 2 4
[6,] 3 4
5. 数值积分梯形法则
梯形法则原理:将被积函数近似为直线函数,被积的部分近似为梯形。
> x = (1:10)*pi/10
> trapz(x, sin(x))
[1] 1.934983
> x = (1:1000)*pi/1000
> trapz(x, sin(x))
[1] 1.999993
6. LogitBoost分类器
取datasets::iris数据集,5列分别是Sepal.Length(花萼长)、 Sepal.Width((花萼宽)、 Petal.Length(花瓣长)、Petal.Width(花瓣宽)、Species(种属)。
> head(iris)
| Sepal | Length Sepal | Width Petal | Length Petal | Width Species |
|---|---|---|---|---|
| 1 | 5.1 | 3.5 | 1.4 | 0.2 setosa |
| 2 | 4.9 | 3.0 | 1.4 | 0.2 setosa |
| 3 | 4.7 | 3.2 | 1.3 | 0.2 setosa |
| 4 | 4.6 | 3.1 | 1.5 | 0.2 setosa |
| 5 | 5.0 | 3.6 | 1.4 | 0.2 setosa |
| 6 | 5.4 | 3.9 | 1.7 | 0.4 setosa |
> Data = iris[,-5]
> Label = iris[, 5]
> model = LogitBoost(Data, Label, nIter=20) #训练模型
> model #模型数据
$Stump
| feature | threshhold | sign | feature | threshhold | sign | feature | threshhold | sign |
|---|---|---|---|---|---|---|---|---|
| [1,] 3 | 1.9 | -1 | 2 | 2.9 | -1 | 4 | 1.6 | 1 |
| [2,] 4 | 0.6 | -1 | 3 | 4.7 | -1 | 3 | 4.8 | 1 |
| [3,] 3 | 1.9 | -1 | 2 | 2.0 | -1 | 4 | 1.7 | 1 |
| [4,] 4 | 0.6 | -1 | 3 | 1.9 | 1 | 3 | 4.9 | 1 |
| [5,] 3 | 1.9 | -1 | 4 | 1.6 | -1 | 4 | 1.3 | 1 |
| [6,] 4 | 0.6 | -1 | 1 | 6.5 | 1 | 2 | 2.6 | -1 |
| [7,] 3 | 1.9 | -1 | 3 | 1.9 | 1 | 4 | 1.7 | 1 |
| [8,] 4 | 0.6 | -1 | 2 | 2.0 | -1 | 2 | 3.0 | -1 |
| [9,] 3 | 1.9 | -1 | 3 | 5.0 | -1 | 3 | 5.0 | 1 |
| [10,] 4 | 0.6 | -1 | 2 | 2.9 | 1 | 1 | 4.9 | -1 |
| [11,] 3 | 1.9 | -1 | 3 | 1.9 | 1 | 3 | 4.4 | 1 |
| [12,] 4 | 0.6 | -1 | 2 | 2.0 | -1 | 4 | 1.7 | 1 |
| [13,] 3 | 1.9 | -1 | 3 | 5.1 | -1 | 2 | 3.1 | -1 |
| [14,] 4 | 0.6 | -1 | 2 | 2.0 | -1 | 3 | 5.1 | 1 |
| [15,] 3 | 1.9 | -1 | 3 | 1.9 | 1 | 1 | 6.5 | -1 |
| [16,] 4 | 0.6 | -1 | 4 | 1.6 | -1 | 3 | 5.1 | 1 |
| [17,] 3 | 1.9 | -1 | 2 | 3.1 | 1 | 2 | 3.1 | -1 |
| [18,] 4 | 0.6 | -1 | 3 | 1.9 | 1 | 1 | 4.9 | -1 |
| [19,] 3 | 1.9 | -1 | 2 | 2.0 | -1 | 4 | 1.4 | 1 |
| [20,] 4 | 0.6 | -1 | 3 | 5.1 | -1 | 2 | 2.2 | -1 |
$lablist
[1] setosa versicolor virginica
Levels: setosa versicolor virginica
attr(,"class")
[1] "LogitBoost"
> Lab = predict(model, Data) #分类预测,Lab只显示分类的结果, Prob显示各分类的概率
> Prob = predict(model, Data, type="raw")
> t = cbind(Lab, Prob) #结果合并,打印前6列
> head(t)
| Lab setosa | versicolor | virginica |
|---|---|---|
| [1] 1 | 1 0.017986210 | 1.522998e-08 |
| [2,] 1 | 1 0.002472623 | 3.353501e-04 |
| [3,] 1 | 1 0.017986210 | 8.315280e-07 |
| [4,] 1 | 1 0.002472623 | 4.539787e-05 |
| [5,] 1 | 1 0.017986210 | 1.522998e-08 |
| [6,] 1 | 1 0.017986210 | 1.522998e-08 |
前6条数据,Lab列表示数据属于分类1,即setosa。其他3列setosa,versicolor,virginica,分类表示属于该分类的概率是多少。下面设置迭代次数,比较分类结果与实际数据结果。
> table(predict(model, Data, nIter= 2), Label) #设置迭代次数为2
|setosa |versicolor |virginica
|---|---|---
setosa 48 | 0 | 0
versicolor 0 | 45 | 1
virginica 0 | 3 | 45
> table(predict(model, Data, nIter=10), Label) #设置迭代次数为10
Label
| setosa | versicolor | virginica |
|---|---|---|
| setosa 50 | 0 | 0 |
| versicolor 0 | 47 | 0 |
| virginica 0 | 1 | 47 |
> table(predict(model, Data), Label) #默认迭代次数, 训练时LogitBoost的nIter值
Label
| setosa | versicolor | virginica |
|---|---|---|
| setosa 50 | 0 | 0 |
| versicolor 0 | 49 | 0 |
| virginica 0 | 0 | 48 |
从上面3次测试结果可以看出,迭代次数越多模型分类越准确。下面随机划分训练集和测试集,并分类预测。
> mask = sample.split(Label) #随机取训练集
> length(which(mask)) #训练集99条记录
[1] 99
> length(which(!mask)) #测试集51条记录
[1] 51
> model = LogitBoost(Data[mask,], Label[mask], nIter=10) #训练模型
> table(predict(model, Data[!mask,], nIter=2), Label[!mask]) #分类预测
| setosa | versicolor | virginica |
|---|---|---|
| setosa 16 | 0 | 0 |
| versicolor 0 | 15 | 3 |
| virginica 0 | 1 | 12 |
> table(predict(model, Data[!mask,]), Label[!mask])
setosa| versicolor| virginica
---|---|---
setosa 17 | 0 | 0 versicolor 0 | 16 | 4 virginica 0 | 1 | 13
7. 快速计算工具runmean
均线在股票交易上非常流行,是一种简单、实用的看盘指标。下面我们对时间序列数据取均线,输出结果如图1-22所示。
> BJsales #取datasets::BJsales数据集
Time Series:
Start = 1
End = 150
Frequency = 1
[1] 200.1 199.5 199.4 198.9 199.0 200.2 198.6 200.0 200.3 201.2 201.6 201.5
[13] 201.5 203.5 204.9 207.1 210.5 210.5 209.8 208.8 209.5 213.2 213.7 215.1
[25] 218.7 219.8 220.5 223.8 222.8 223.8 221.7 222.3 220.8 219.4 220.1 220.6
> plot(BJsales,col="black", lty=1,lwd=1, main = "Moving Window Means")
> lines(runmean(BJsales, 3), col="red", lty=2, lwd=2)
> lines(runmean(BJsales, 8), col="green", lty=3, lwd=2)
> lines(runmean(BJsales,15), col="blue", lty=4, lwd=2)
> lines(runmean(BJsales,24), col="magenta", lty=5, lwd=2)
> lines(runmean(BJsales,50), col="cyan", lty=6, lwd=2)
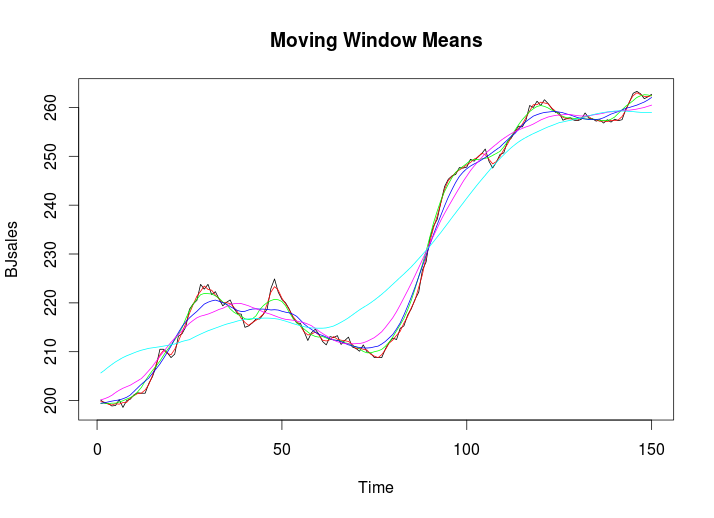
图1-22 时间序列数据的均线图
我们从图1-22中看到6条线, 黑色是原始数据,其他各种颜色线代表不同单位的均线。比如,红色(red)线表示3个点的平均,绿色(green)线表示8个线的平均。
8. 快速计算工具组合
对数据集取最大路径runmax、最小路径runmin、均值路径runmean和中位数路径runmed,输出结果如图1-23所示。
> n=200;k=25
> set.seed(100)
> x = rnorm(n,sd=30) + abs(seq(n)-n/4)
> plot(x, main = "Moving Window Analysis Functions (window size=25)")
> lines(runmin (x,k), col="red",lty=1, lwd=1)
> lines(runmax (x,k), col="cyan",lty=1, lwd=1)
> lines(runmean(x,k), col="blue",lty=1, lwd=1)
> lines(runmed (x,k), col="green",lty=2, lwd=2)
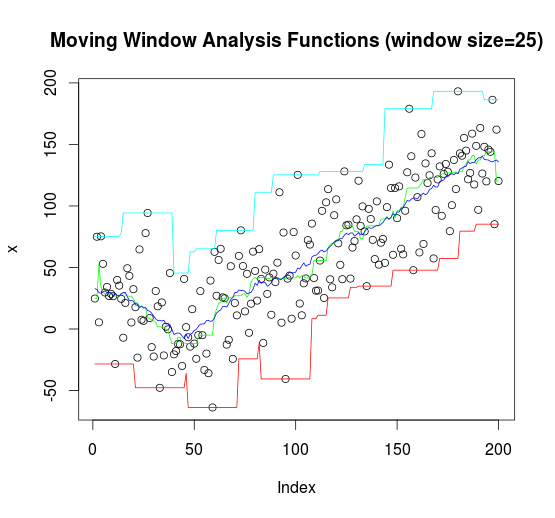
图1-23 路径图
这次我们取4种不同的路径,分别是最大路径、最小路径、均值路径和中位数路径。
9. 无误差求和
各种编程语言,用计算机做小数计算的时候,都会出现计算误差的情况,R语言也有这个问题。首先用sum函数求和。
> x = c(1, 1e20, 1e40, -1e40, -1e20, -1) #计算误差求和
> a = sum(x); print(a)
[1] -1e+20
> b = sumexact(x); print(b) #无计算误差求和
[1] 0
我们对向量x求和,各组值加起来正好为0。但是sum函数,结果是-1e+20,这是由于编程精度的问题造成的计算误差。通过sumexact函数修正后,就没有误差了。下面用cumsum函数累积求和。
> a = cumsum(x); print(a) #计算误差累积求和
[1] 1e+00 1e+20 1e+40 0e+00 -1e+20 -1e+20
> b = cumsumexact(x); print(b) #无计算误差累积求和
[1] 1e+00 1e+20 1e+40 1e+20 1e+00 0e+00
cumsum同样出现了精度的误差,需要用cumsumexact来修正。
最后还是要用“奇特”来概括这个工具集,相信你也发现了他的奇特。